
こんにちは、なおしー(@naoc2520) です!
野球がお好きな方なら一度は聞かれたことがあると思います「日本シリーズ何勝何敗でどっちが勝つと思う?」という質問。
野球解説者の方もテレビでよく答えていますよね。
今日はこの質問に対する妥当な回答をセンター数学の知識を使って考えたいきたいと思います。
準備
まずは日本シリーズのルールを紹介します。
2つの野球チーム A, B が試合を7回行い、先に4勝したほうを優勝とする。
ただし、どちらかのチームが4勝に達した時点で残りの試合は行わない。
簡単に文章にするとこういうことですね。
このルールから考えると日本シリーズの終わり方には
- 4勝0敗
- 4勝1敗
- 4勝2敗
- 4勝3敗
の4パターンがあります。
この4パターンのうち、どの結果になる確率が一番高いのでしょうか?
それではここからは数学の時間、Aが勝つ確率を p として話をすすめて行きたいと思います。
A, B の実力が五分(p =1/2)の場合
はじめに A, B の実力が五分、つまりAが勝つ確率 p = 1/2 の場合を考えてみましょう。
4勝0敗で終わる場合
これは4連勝する場合しかありません。
つまり1/2の確率が4回連続で起こるということです。
A が4連勝する場合を考えると
(1/2)^4 = 1/16
となります。(^4は4乗の意味)
一方今はBが勝つ確率も 1/2 なので、同様にBが4連勝する確率も 1/16 になります。
つまり4勝0敗で終わる確率は
1/16 + 1/16 =1/8 (=0.125)
ということになります。
4勝1敗で終わる場合
次は4勝1敗で終わる場合です。
まずはAが4勝1敗で優勝する場合を考えます。
Aが優勝して終わるので、最終戦(第5戦)はAが勝つことになります。
第4戦が終わった時点ではAの3勝1敗となって、第5戦でAが勝つという寸法です。
では、第1戦から第4戦の星取りが何通りあるかを数えましょう。
これは
A A A B
A A B A
A B A A
B A A A
の4通りがあります。
今はAが勝つ確率もBが勝つ確率も1/2なので上の4通りになる確率はいずれも
(1/2)^4=1/16
です。
つまり1/16 が4通りなのでAが3勝1敗で第5戦を迎える確率は
4×1/16 = 1/4
となります。
さいごに第5戦でAが勝つ確率をかけると、Aが4勝1敗で優勝する確率は
1/4 × 1/2 = 1/8
となります。
ここまでくれば B が4勝1敗で優勝する場合も同様なので 1/8
つまり4勝1敗で終わる確率は
1/8 + 1/8 = 1/4 (=0.25)
ということになります。
4勝2敗で終わる場合
続いて4勝2敗で終わる場合。
これもAが優勝する場合を考えて、基本的には4勝1敗と同じ流れで求めます。
第6戦はAが勝つのでそれまでの第1戦から第5戦までの星取りが何通りあるかですね!
先ほどのように全て羅列してもいいですが、ここでセンター数学で必要な知識を使いましょう。
第5戦までの星取りのパターンはAを3個とBを2個をランダムに並べた時の並び方のパターンに一致します。
これは同じものを含む順列の考え方です。
こういう記号を使って計算したことがあると思います。
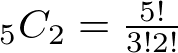
この計算結果は10になります。
さらにこの10通りになる確率はいずれも
(1/2)^5=1/32
であり、第5戦までをAが3勝2敗で終える確率は
10 × 1/32 = 5/16
となります。
最後の第6戦でAが勝つ確率をかけると、4勝2敗でAが優勝する確率は
5/16 × 1/2 =5/32
となります。
Bが4勝2敗で優勝する確率も同様に5/32なので、
4勝2敗で終わる確率は
5/32 + 5/32 =5/16(=0.3125)
となります。
4勝3敗で終わる場合
長くなっていますが、最後に4勝3敗の場合です。
これも同様にAが優勝する場合を考えましょう。
さらに、同じものを含む順列の考え方も使います。
第6戦までにA, Bがそれぞれ3勝ずつですから、Aを3個とBを3個ランダムに並べて数えましょう。
この並べ替えの数は
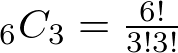
を計算して20通りとなります。
さらにこの20通りになる確率はいずれも
(1/2)^6 = 1/64
であり、第6戦までをAが3勝3敗で終える確率は
20 × 1/64 = 5/16
となります。
最後の第7戦でAが勝つ確率をかけると、Aが4勝3敗で優勝する確率は
5/16 × 1/2 = 5/32
となります。
Bが4勝3敗で優勝する確率も同様に5/32なので、
4勝3敗で終わる確率は
5/32 + 5/32 =5/16(=0.3125)
となります。
まとめ
以上をまとめると次のようになります。
4勝0敗 1/8 (=0.125)
4勝1敗 1/4 (=0.25)
4勝2敗 5/16(=0.3125)
4勝3敗 5/16(=0.3125)
ということで、AとBの勝つ確率が同じ場合は4勝2敗か4勝3敗になる確率が最も高いということになります。
Aの方がちょっと勝つ確率が高かった場合(p=3/5)
ここからはちょっと発展系。
先ほどは実力伯仲の場合を考えましたが、そうではなかった場合どうなるのかを考えたいと思います。
Aが勝つ確率をちょっと高めて 60% つまり p=3/5 にしてみます。
計算は基本的に p=1/2 の場合と同じですが、AとBの勝つ確率が異なる(Bは40%)ので「同様に~」のところが使えないので注意が必要です。
ここは結果だけ紹介したいと思います。
4勝0敗 97/625 (=0.155…)
4勝1敗 168/625 (=0.2688)
4勝2敗 936/3125(=0.2995…)
4勝3敗 864/3125(=0.276…)
となります。
つまり、Aの方がちょっと勝つ確率が高かった場合は4勝2敗で終わる確率が最も高いということになります。
p が変わるとどうなるか?
とりあえず A の勝つ確率が 50% と 60% の場合についてやりましたが、他の確率の場合はどうなるのでしょうか?
Aの勝つ確率がどの程度高くなれば4勝1敗で終わる確率が最も高くなるのでしょうか?
このようなことを調べる場合はグラフを書いてみるのが一番です。
確率を p のままにして式を立ててみると
4勝0敗で終わる確率は p^4 + (1-p)^4
4勝1敗で終わる確率は 4{p^4(1-p)+(1-p)^4p}
4勝2敗で終わる確率は 10{p^4(1-p)^2+(1-p)^4p^2}
4勝3敗で終わる確率は 20{p^4(1-p)^3+(1-p)^4p^3}
となり、これでグラフを書いてみると次のようになります。
横軸が x のままなのは無視してください。
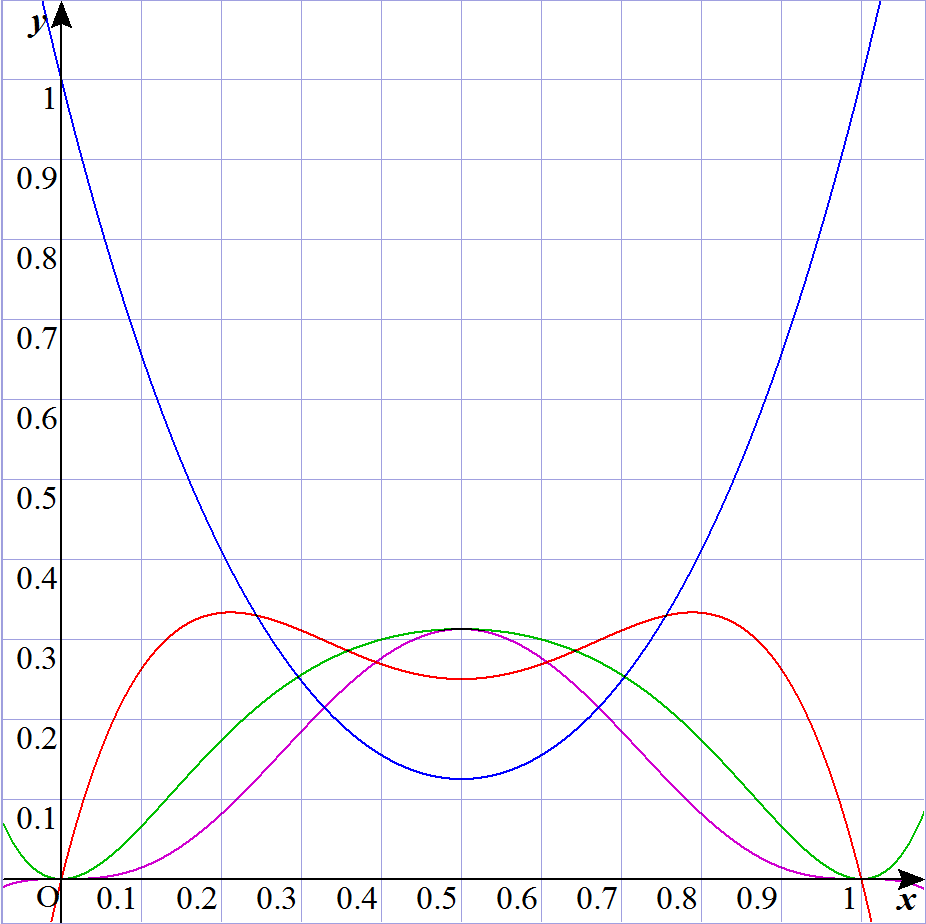
p=1/2 で対称になるのは当然ですね。
こうやって見ると、p=1/2 の付近では4勝2敗の確率が高いですね。
また、4勝3敗の確率が最も高くなるのは p=1/2 のときのみというのもわかりました。
そして、4勝1敗で終わる確率が最も高くなるのは p=0.65 付近からということもわかります。
これを踏まえると最も無難に正解できそうな答えは4勝2敗ということになるでしょう。
実際の戦績では?
それでは数学のお話ではなく実際の戦績を見てみましょう。
こちらのサイトの結果から集計しました。
2016年まで過去66回行われた日本シリーズの星取り結果を集計して見た結果は以下のとおりです。
4勝0敗 7回
4勝1敗 16回
4勝2敗 22回
4勝3敗 21回
ということで、実際の結果でも4勝2敗で終わった回数が最も多いということでした。
まとめ
計算結果と過去の戦績の両方で4勝2敗と答えるのが最も当たる確率が高いようです。
センター数学と言っておきながら高校数学の知識は導入くらいしか使いませんでしたね。
現役の高校生にはこれくらいすんなりといてほしいと思います。
ちなみにどちらが勝つかはこんな簡単な計算では求まりません。
とりあえず4勝2敗と言っておいて、結果か出たら星取りだけは当たったでしょと言っておきましょう。
もっと確率を上げるとなれば「接戦になると思うから4勝3敗か4勝2敗かな」と言っておけば計算上6割5分近くの確率で当たることになります。
第2弾、第3弾はこちらです!