こんにちは、なおしー(@naoc2520) です!
突然ですが、プロ野球を見ているとこういうプレーって時々ありますよね。
こういったプレーの場合、ランナーがホームに突入するかどうかというのをランナーコーチという人が判断しています。
この画像では無視されていますが、74番の人がランナーコーチです。

点差などの試合状況だけでなく外野手の捕球位置や肩の強さ、走者の走力などからランナーをサードで止めるかホームに向かわせるかを判断しています。
プレイヤーではないので地味に見えますが、1点を争うプレーに関わるため意外と重要な役割です。
今日はこの判断材料の一つ、ゴロヒットの場合の外野手の捕球位置をセンター数学の知識を使って計算で求めてみたいと思います。
準備
計算を簡単にするために、打球と外野手の動く速さは次の数値で一定とします。
打球の速さは126km/h=35m/s
外野手の速さは5m/s
とします。
どの数値で一定にするかについては次のサイトを参考にしました。
打球速度を伸ばすには | 倉俣監督BLOG | スポーツナビ+
スプリントスピード強化のトレーニングとタイム計測テクノロジーの活用(1)
それでは外野手を配置しましょう。
今回は前の動画と同じレフトで考えたいと思います。
レフトははじめのポジショニングでレフト線から 24.5m, ライト線から 73.5m の位置にいるものとします。
図で表すとこんな感じです。
左下の原点がホームで、四角の枠はベースを繋いでできるものだと思ってください。
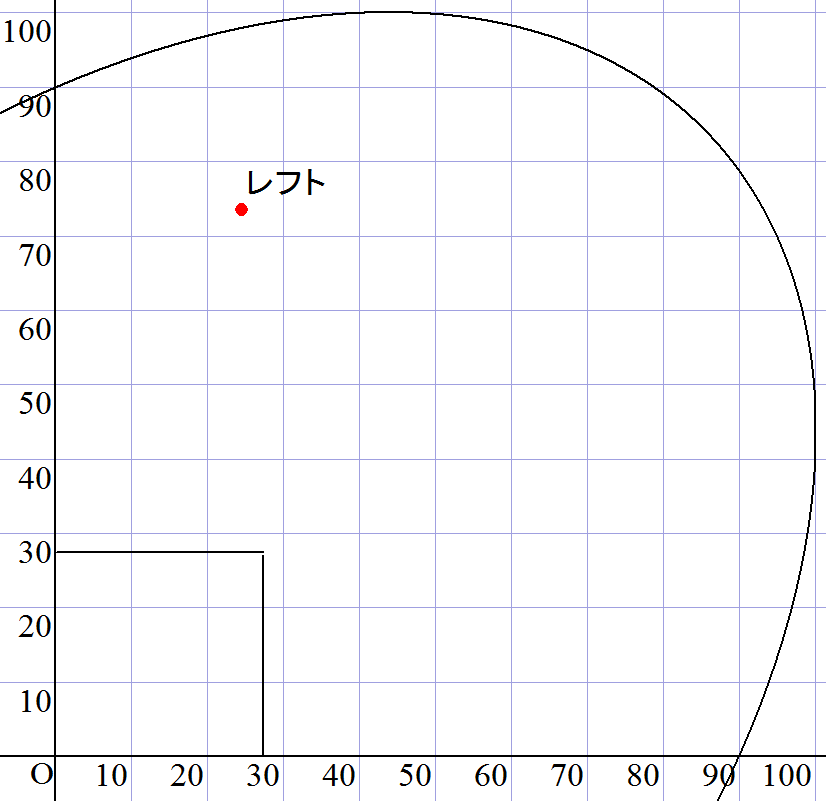
外野フェンスの形は一応両翼90mとセンター120mは通っていますが、実際とかなり異なると思います。
外野手の捕球する位置は?
それでは準備で決めた状況のもとでレフトが捕球する位置を求めてみたいと思います。
外野手と打球の速さはそれぞれ 5m/s と 35m/s だったので、速さの比は1:7ということになります。
速さの比は距離の比に一致するので、これからわかることは
(守備位置から捕球位置までの距離):(ホームから捕球位置までの距離)
=1:7
ということです。
つまり捕球位置は、守備位置とホームベースからの距離の比が1:7の点の集まりということになります。
これは高校数学の軌跡の方程式という単元の考え方で求めることが出来ます。
実際に計算してみた
ホームの位置を O(0, 0)、レフトの守備位置を点 L(24.5, 73.5)、捕球する点 C(X,Y)とします。
このときホームから捕球位置までの距離OCと、レフトの守備位置から捕球位置までの距離LCはそれぞれ
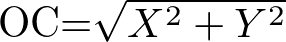
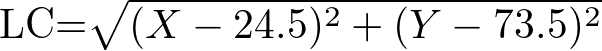
となります。
LC:OC=1:7ですから
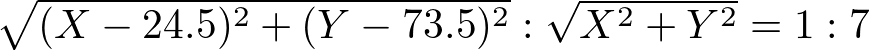
このような比の式が立ちます。
これから高校までの知識で式を変形していくと次のような形になります。
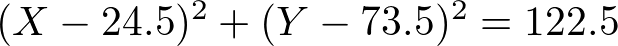
この式のグラフを先程の図に書き加えてみるとこのような形になります。
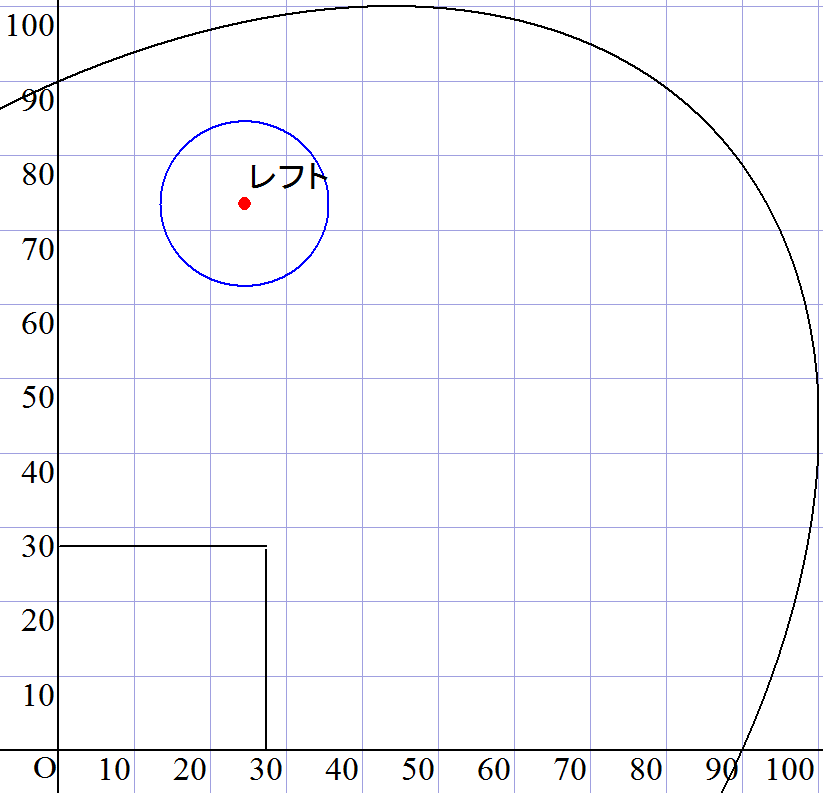
察しの良い方はもともとの条件からわかるかもしれませんが、計算上の外野手の捕球位置はこの円周上の何処かということになります。
実際には守備位置より後ろでゴロを捕球することはないので、下半円の内部と円周上くらいになると思います。
計算しやすいように条件をかなり補正しましたが、根本の考え方は高校数学の範囲で十分です。
まとめ
これくらいの計算ならばコンピュータで一瞬でしょう。
外野手の速さは予めデータとして準備しておいて、打球の速さをスピードガンなんかで計測すれば一瞬で捕球位置の候補となる円は求められると思います。
さらに、走者の走力と外野手の肩の強さ(送球の速さ)もデータとして持っておけばランナーコーチの仕事は自動化できるかもしれません。
ちなみに今回は第2弾で、第1弾、第3弾もありますよ!