こんにちは、なおしー(@naoc2520) です!
野球の華といえばホームランですよね。
侍ジャパンの4番候補であるDeNA筒香嘉智選手は2016シーズンに44本のHRを放ちました。
HR王を獲得したので44本という本数が話題になりましたが、それと合わせてよく言われるのがHRの飛距離です。
筒香選手がジャストミートした打球は横浜スタジアムなら場外になるほどの飛距離を記録することもあります。
ということで今日は、場外の場合には使えないかもしれませんがセンター数学の知識を使ってHRの飛距離の計測方法を考えてみたいと思います。
準備
まずはいろいろと準備をしていきますしょう。

上の図のようにホームベースの位置をO、打球の着弾点をHとします。
そして場外にA, Bという2点を用意して、ここにそれぞれ計測者を置きます。
今回のキモはこの2人の計測者です。
この2人が何を計測するかというと上の図で★ ■ ● で示した3つの角の大きさです。
一応記号で表すとそれぞれ
★ = ∠OAH
■ = ∠HAB
● = ∠ABH
を表しています。
HRが出た瞬間にこの3つの角の大きさを計測してもらいます。
それから、あらかじめホームベースからAまでの距離OAとAからBまでの距離ABを図っておく必要があります。
実際には難しいかもしれませんが、場外だし試合前ならできるということで勘弁してください。
手順としては上の画像のAH(青線)の距離を正弦定理で求めてから求めたい飛距離であるOH(赤線)の距離を余弦定理で求めたいと思います。
計算してみた
それでは実際に例題を示して計算してみたいと思います。
Aをホームベース後方10mの位置に、Bをそこから90m離れた位置に配置します。
そして、計測した結果が次のようになった場合を考えましょう。
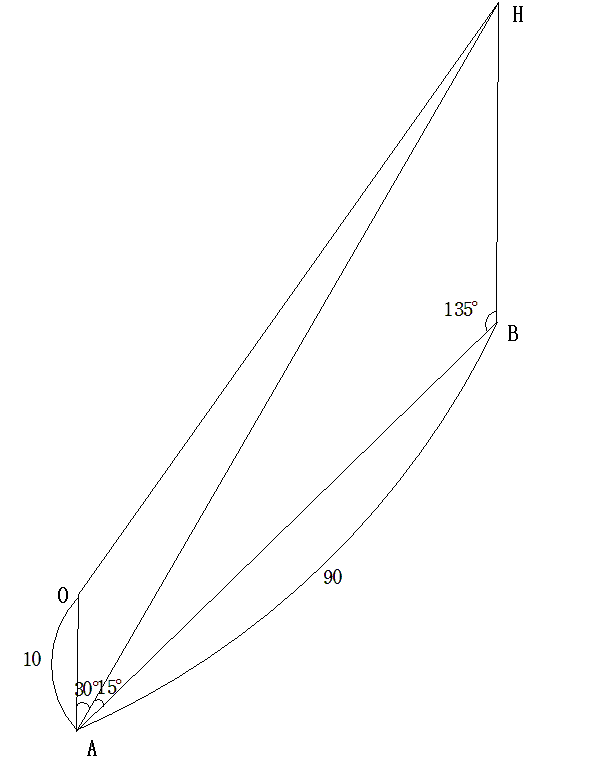
手順をおさらいすると
- AHを⊿ABHにおける正弦定理を用いて求める
- OHを⊿OAHにおける余弦定理を用いて求める
の2段階方式です。
まずは正弦定理を使ってAHを求めます。
正弦定理を使うために∠AHBを求めます。
三角形の内角の和は180°なので、
∠AHB=180°-15° - 135° = 30°
となります。
ここから、いよいよ正弦定理を使うとこのような式が立ちますね。
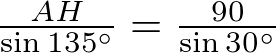
サインの値は高校生の時に暗記していると思うので、それを代入しましょう。
そんなもん忘れたという方はコチラから
0°,30°,45°,60°,90°,120°,135°,150°,180°の三角比の値をまとめた表 / 数学I by ふぇるまー |マナペディア|
これを代入して計算すると
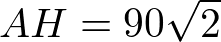
となります。
これでいよいよ求めたい飛距離OHにいきたいと思います。
余弦定理を使うと次のように式が立ちます。
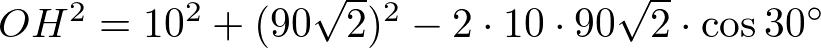
これを計算すると
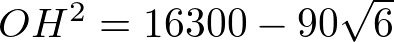
だから

となります。
二重根号になってしまったので電卓を使って計算するとOH=126.80…でした。
今回の場合は約127メートルのHRということですね。
まとめ
今回は高校数学の範囲でHRの飛距離を計算してみました。
もしかすると高校数学というよりは測量とかに近いのかもしれません。
距離はメジャーを張らないと測れませんが、角度はその場で測れるという性質を使っています。
実際にはこんなきれいな角度になるわけがないので、三角比の表などを使うことになるでしょう。
ちなみに A, B の位置はそのままでレフト方向でも同じ方法で計測することが出来ます。
それから奇跡的にド正面に打ち返された場合は2段階の手順を踏むことなく正弦定理だけで求めることが出来ます。
といっても、現代の技術ではこんな計算をすることすら必要ないんでしょうけどね。
ゴルフ用ですが覗くで距離を測ってくれるようです。
今回は「センター数学×野球」の第3弾です。
意外と読まれている関連記事はコチラです。
